In der Nacht auf den 12. Dezember 1978 hat das 260 Meter lange Containerschiff »München« im Nordatlantik mit schwerem Seegang zu kämpfen. Der 28-köpfigen Besatzung saust eisiger Wind mit über 110 Stundenkilometern um die Ohren; am nahen Horizont türmen sich meterhohe Wellen auf.
Doch erfahrene Seeleute lassen sich nicht aus der Ruhe bringen. So wirkt der Funker des Tankers entspannt, als er seinem Kollegen auf dem Kreuzfahrtschiff »Caribe« kurz nach Mitternacht mitteilt: Wir haben schlechtes Wetter. Brücke ist beschädigt, Bullaugen eingeschlagen.
Laut Hapag-Lloyd, der Reederei der »München«, beenden die Funker ihr Gespräch mit gute Fahrt und bis demnächst
.
Dazu sollte es nicht kommen. Gut drei Stunden später, um 3:30 Uhr, funkt die »München« SOS. Das Schiff sinkt. Zehn Tage lang suchen etwa 100 Schiffe nach dem Tanker; mehr als zehn Flugzeuge umkreisen die Gegend nördlich der Azoren, in der sie ihn vermuten. Drei Container, ein Rettungsboot, eine Notfunkbake und ölverschmierte Rettungsinseln sind alles, was die Helfer finden. Bis heute fehlt vom Wrack und der Besatzung jede Spur. Die »München« scheint wie vom Meer verschluckt.
Und vielleicht wurde sie das tatsächlich. Schäden am geborgenen Rettungsboot deuten später darauf hin, dass die »München« von einer sogenannten Monsterwelle getroffen wurde. Monsterwellen sind selten, sie können selbst bei ruhiger See entstehen und messen von Wellental zu Wellenkamm bis zu 35 Meter. Ozeanografen definieren sie als Wellen, die mehr als doppelt so hoch sind wie der Durchschnitt des höchsten Drittels der benachbarten Wellen.
Seeleute nennen die gigantischen Brecher Kaventsmänner, seit Jahrhunderten erzählen sie Schauergeschichten über die riesigen Ungetüme. Lange jedoch tat die Fachwelt ihre Berichte als Seemannsgarn ab. Erst als 1995 auf einer Ölplattform in der Nordsee eine 26 Meter hohe Monsterwelle mit moderner Lasertechnik gemessen wurde, nahm die Fachwelt die Geschichten der Seefahrer ernst.

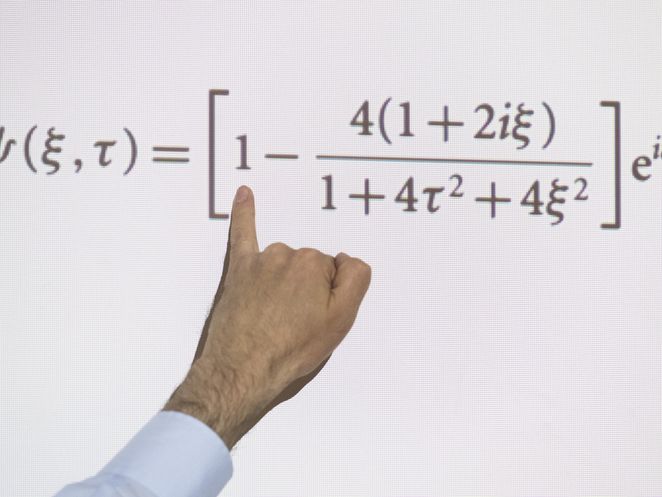
Seither stürzen sich Forscher auf das Phänomen Monsterwelle. Physiker wissen, dass es im Universum eine große Vielfalt an Wellen gibt. Geräusche (also Schall), Wärmestrahlung, Licht und seismische Aktivität lassen sich physikalisch allesamt als Wellen auffassen. Die Frage lag also auf der Hand: Wenn in den Weltmeeren gewaltige Brecher tatsächlich Schiffe versenken, tauchen diese Monsterwellendann auch anderswo auf?
Tatsächlich weist im Jahr 2007 ein Forschungsteam um den Physiker Daniel Soli nach, dass sich auch kleinste Lichtwellen zu verhältnismäßig riesigen Wellenbergen auftürmen können – was dazu führen kann, dass sich die wahrgenommene Farbe des Lichts ändert. Mehr noch: Diese optischen Monsterwellen lassen sich in Kristallfasern mit den richtigen Impulsen gezielt erzeugen. Später werden Monsterwellen auch in flüssigem Helium, bei Wärmestrahlung und in Mikrowellen entdeckt.
Was Physikerinnen und Physiker besonders fesselt: Die winzigen optischen Wellen scheinen dabei den gleichen Regeln zu gehorchen wie ihre großen Schwestern in den Weltmeeren. Die Fachwelt ist doppelt entzückt: praktisch, weil die Forscher fortan mit Lichtwellen in Glasfaserkabeln experimentieren können, um etwas über Kaventsmänner im Ozean zu lernen. Theoretisch, weil Physiker stets versuchen, mit möglichst einfachen Gesetzen möglichst viele Phänomene in der Natur zu erklären. Diese Gesetze, so sind sie überzeugt, bestehen aus mathematischen Gleichungen. Das Universum ist in der Sprache der Mathematik geschrieben
, proklamierte Galileo Galilei. Und wer diese nicht beherrsche, der irre in ihm umher wie in einem dunklen Labyrinth.
Shalva Amiranashvili kennt Teile dieses Labyrinths wie seine Westentasche. Der Physiker weiß, wie Monsterwellen scheinbar aus dem Nichts entstehen und dann spurlos wieder verschwinden. Und er hat mit seinen Kollegen herausgefunden, wie sie von kleineren Wellen mit Energie versorgt werden – und warum sie deutlich öfter auftauchen als vermutet. Amiranashvili forscht am Weierstraß-Institut für Angewandte Analysis und Stochastik (WIAS), einem mathematischen Leibniz-Institut in der Mitte Berlins, und gilt als einer der führenden Experten auf dem Gebiet der optischen Monsterwellen. Er hat schon einige Ausgänge aus Galileis Labyrinth gefunden – auch wenn es manchmal ein paar Jahre gedauert hat und er gar nicht mehr auf der Suche nach dem Ausgang war. Doch dazu später mehr.
Wer Shalva Amiranashvili am WIAS besucht, muss nicht lange auf ihn warten. Überpünktlich erscheint der Physiker an diesem Maimorgen in hellblauem Hemd, schwarzer Hose und unauffälligen Lederschuhen im Foyer des Instituts und begrüßt Fotografen und Reporter. Amiranashvili führt geduldig durch die Flure des Instituts; er schweigt meist, doch wenn er redet, hat er etwas zu sagen. Es sprudelt dann nur so aus ihm heraus. Der 57-jährige Georgier spricht blitzschnelles, fast perfektes Deutsch, auch wenn er seine Sprachkenntnis selbst als »Ausländerdeutsch« bezeichnet.


Geboren wurde Shalva Amiranashvili 1964 als Sohn eines Historikers und einer Physikerin in Tiflis, der heutigen Hauptstadt Georgiens. Mathematik und Physik fallen dem kleinen Shalva leicht; früh knobelt er in landesweiten Wettbewerben mit Erfolg an mathematischen und physikalischen Problemen. Nach der Schule möchte er in Moskau Physik studieren; die Aufnahmeprüfung gilt als die härteste der Sowjetunion. Im Mathe-Teil der mündlichen Prüfung weiß das Ausnahmetalent zum ersten Mal nicht weiter. Wie man ein beliebiges Viereck in zwei gleich große Teile teilt, will ihm nicht einfallen; umso enthusiastischer grübelt Amiranashvili – ohne Erfolg.
Vier Jahre später, während er sich in einem Statistik-Seminar langweilt, wabert die Geometrieaufgabe noch immer in seinem Hinterkopf herum – da trifft ihn plötzlich ein Geistesblitz: Er löst das Problem, indem er einen gedanklichen Umweg über Dreiecke nimmt. Auch seine nach eigener Einschätzung schönste wissenschaftliche Entdeckung am WIAS sollte Amiranashvili später machen, als er schon nicht mehr daran glaubte. Bei der Aufnahmeprüfung glänzt er übrigens trotzdem, er studiert und promoviert in Moskau. Nach dem Zusammenbruch der Sowjetunion verlässt er das Land und landet über einen Umweg nach Bochum und Münster am Weierstraß-Institut in Berlin.
Im Büro des Wellenforschers stehen drei Tische, drei Stühle, drei Bildschirme, eine Handvoll Bücher. Mehr brauchen Amiranashvili und seine Kollegen nicht. Wer erwartet hat, dass der Physiker Wellen durch Wassertanks jagt oder im Labor an Lasern herumbastelt, wird enttäuscht. Amiranashvili bricht Wellen nur im Kopf – und in den Computern des institutseigenen Rechenzentrums, wo die WIAS-Wissenschaftler Wellen simulieren. So bestätigen oder widerlegen sie ihre mathematischen Theorien, die sie mit Bleistift, Papier und jeder Menge Vorstellungskraft am Schreibtisch entwerfen.
Seine schönste Entdeckung machte er, als er schon nicht mehr daran glaubte.
Zu zwei mathematischen Werkzeugen greifen die Wellenforscher dabei oft: Fourier-Transformation und Differentialgleichungen. Das erste Werkzeug nutzen sie, um Ordnung in die chaotisch wirkenden Wellenberge in der Natur zu bekommen. Die Fourier-Transformation erlaubt es, Wellen in Sinuskurven aufzuteilen. Sinuskurven kennt jedes Schulkind, sie oszillieren gleichmäßig um ein festes Niveau mit gleichbleibender Frequenz – immer hin und her zwischen Wellenberg und Wellental. Das Geniale an der Fourier-Zerlegung ist also, dass sie Wellen in ihre Frequenzanteile aufteilt, also zum Beispiel ein Tonsignal (Schallwellen) in die verschiedenen Tonhöhen, aus denen es sich zusammensetzt. Sie gilt als eine der wichtigsten Ideen der angewandten Mathematik überhaupt.
Zum zweiten Werkzeug greifen Wissenschaftlerinnen und Wissenschaftler, wenn sie Veränderungen in der Natur modellieren – von der Bewegung von Planeten bis hin zum Wachstum von Bakterienkulturen in einer Petrischale. Differentialgleichungen beschreiben eine Funktion damit, wie sie mit ihrer Ableitung zusammenhängt. Was war das nochmal, eine Ableitung? Diese Frage habe der Physiker William Thomson Kelvin seinen Studierenden auch einmal gestellt, erzählt Amiranashvili. Die Studierenden überboten sich mit mathematischen Definitionen. Kelvin schüttelte den Kopf: Ableitung ist Geschwindigkeit.
Wenn eine Funktion zum Beispiel angibt, wie weit ein Containerschiff zu einem bestimmten Zeitpunkt gefahren ist, dann ist die Ableitung dieser Funktion die Geschwindigkeit. Diese konkrete Vorstellung liebe ich an der Physik
, sagt Amiranashvili. Eine Differentialgleichung zu lösen, ist dann nichts weiter, als eine Funktion zu finden, die angibt, wie weit das Schiff in einer bestimmten Zeit gekommen ist, wenn bekannt ist, wie seine Geschwindigkeit mit der zurückgelegten Strecke zusammenhängt.
Eine für Amiranashvili und seine Kollegen besonders wichtige Differentialgleichung ist die nichtlineare Schrödingergleichung. Mit ihr beschreiben sie die Veränderung von Enveloppen; das sind Funktionen, die Wellen von oben und unten einhüllen. Sie verbinden also einerseits die Gipfel aller Wellenberge und andererseits alle Tiefpunkte der Wellentäler miteinander. Früher dachte man, durch simple Überlagerung mehrerer Wellen könnte man die Entstehung riesiger Wellen erklären. Mittlerweile ist klar, dass dazu komplexe Differentialgleichungen wie die Schrödingergleichung nötig sind

Dennoch sagten die darauf basierenden Modelle seltener monströse Lichtwellen voraus, als beobachtet wurden. Denn sie vernachlässigten ein faszinierendes Schauspiel: Während sich die monströse Wellenwand fortbewegt, prallen kleinere Wellen teilweise wie an einem Spiegel an ihr ab. Dabei füttern sie die Monsterwelle mit Energie. Vor etwa zwölf Jahren beobachtete Shalva Amiranashvili zusammen mit seinen Kollegen Ayhan Demircan und Günter Steinmeyer vom Max-Born-Institut für Nichtlineare Optik und Kurzzeitspektroskopie das Spektakel zum ersten Mal. Wir waren überrascht, wie schnell eine Welle Energie von ihren kleineren Nachbarinnen aufnehmen kann.
Später, nach einigen Umwegen, gelang es ihm, dieses Phänomen zu modellieren – gemeinsam mit seiner damaligen Kollegin Sabrina Pickartz und seinem Chef Uwe Bandelow. Ihren mathematischen Werkzeugkasten mussten sie dazu mühevoll erweitern. Wir haben zwei Jahre lang gekämpft
, sagt Amiranashvili.
Ihr Modell hilft dabei, optische Monsterwellen besser zu verstehen. Bis auch die Kaventsmänner auf hoher See vorhergesagt werden können, ist es zwar noch ein weiter Weg. Zu viele Faktoren sind noch unbekannt, zu wenige Daten vorhanden. Doch eines Tages könnten so Schiffsunglücke wie das der »München« verhindert werden. Aber auch im Licht selbst findet die Arbeit der WIAS-Forscher fruchtbare Anwendung. Wenn Sie diesen Text später noch einmal im Internet lesen, dann ist er eventuell als Lichtwelle durch ein Glasfaserkabel bei Ihnen angekommen. Hierbei zittern die Takte der Übertragung manchmal, was den Datentransfer verlangsamt. Amiranashvilis Forschung könnte dazu beitragen, diese Störsignale zu reduzieren.
Noch keine Anwendung gibt es für eine Entdeckung, die Amiranashvilis Augen noch immer funkeln lässt, wenn er von ihr erzählt. Fünf Jahre nachdem er die Reflexion kleiner Wellen an der Monsterwelle erforscht hatte, blickte er noch einmal auf die Grafiken von damals. Auf einmal sah er es: Weil die Riesenwelle eine gebogene Form hat, bündeln sich die reflektierten Wellen an einer Stelle wie zu einer Brennlinie. Das »Kaustik« genannte Naturschauspiel kennt man von tanzenden Lichtlinien in flachem Wasser.
Heute ist es dem Physiker ein Rätsel, wie er diese anmutigen Muster in den Lichtwellen so lange übersehen konnte. Das war wie bei der Geometrieaufgabe – die dümmste Art, eine Entdeckung zu machen
, sagt Amiranashvili. Man könnte auch sagen: die schönste. Schließlich kam sie aus dem Nichts – wie so manche Monsterwelle.